图像卷积
从公式引入
$\int _{-∞}^∞ f(τ)g(x-τ)dτ$
简例:
假设有一个系统,全天不间断输入不定量的能量,同时按某个曲线消耗能量
某时刻输入量与时间关系为 $f(x)$ ;同时,每一份能量的剩余比例与输入后时间关系为 $g(x)$
对于时间点 $τ$ 的能量输入,在时间为 $x$ 时剩余量为 $f(τ)g(x-τ)$
- 设 $x$ 为总的能量输入时间轴,求 $t$ 时刻总的剩余能量—— $\int _0^t f(x)g(t-x)dx$
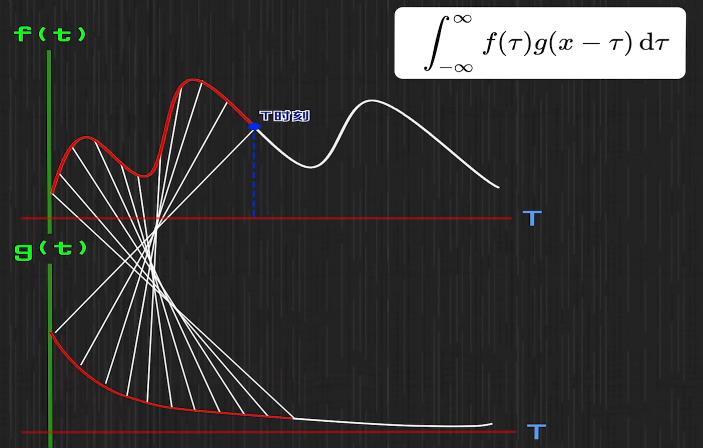
一个时间点的总能量,是过去每个时间点输入能量的积分
而被积分的是两个函数,他们的参数分别是一个时间点和一个时间差,且导数恰相反

- 若将以上积分的时间上下限由 0 ~ $t$ 改为无穷大,就得到了标准的卷积公式
图像的卷积
对像素矩阵使用 3*3 卷积核,最外圈为 0,每次卷积核移动时,重叠位置相乘后并求和,保存在中心位置
相当于卷积核每次移动,都会求一次 3*3 区间内函数相乘结果的积分
进一步理解
抽象一下,就变成——
某个变量会产生影响,随着一定因素会不断变化、累积。$33$ 卷积核的作用就是计算周围一圈像素对当前像素影响的结果。一般如果 $33$ 能清楚反映整体特征就不会考虑更大的卷积核
例如,9 个 1/9 的卷积核,可以对每个 3*3 区域求平均值,最终效果就是让图像平滑
设定点像素为 $(m,n)$,显然整个图像每个点当前的值是 $f(x,y)$,周围点的影响可以设为 $g(m-x,n-y)$。每个像素点卷积后的值就是离散的 $\sum f*g$
当前点设为 $(x,y)$,取左下角 $(x-1,y-1)$
则 $f*g=f(x,y)g(x-(x-1)),y-(y-1))=f(x,y)g(1,1)$
可以发现,卷积后呈现的 $g$ 被翻到了右上角
出于计算机考虑,将翻转后的 $g$ 定义为卷积核,至此卷积的初步认识达成
卷积神经网络
卷积神经网络可以说就是用于图像识别的
相比于平滑卷积核,通过修改每个位置的系数,可以试探并专门捕捉和筛选周围一圈特定形式的排列
处理后的图像只保留了描述特征的数值矩阵,交由神经网络处理
总结
- 卷积可以对不稳定的输入得到稳定的输出值
- 用于图像处理,可以捕捉图像局部特征
神经网络
感知机与神经网络
神经网络的始祖,对数据进行分类。给数据训练,并实时调整分界线,对于更多特征的分类则为分界面等
说白了要得到一个变量对应维度的超平面。因此感知机的表达式为
$$t=f(\sum^n_{i=1}w_ix_i+b)=f(W^TX)$$ W X 是 n 维向量,第一维的值是 b 和 1
两个部分又叫线性函数和激活函数
50年前人们发现了感知机的致命缺陷——无法用各种各样的曲线特别是圆圈做分类
但对于现在的学生,都不算是问题了——
多个感知机组合为异或结构,分两层,每一层都是单个逻辑运算,每次只需根据前一步的输入确定标准线
先在底层输入 x,经过两层网络得到结果
于是,神经网络雏形初现,感知机就是“神经元”,输入多个数据,输出一个标准线
神经网络
基本结构
输入层——隐藏层——输出层,每层都能有多个结点
分类方式例
全连接神经网络(每个结点都接收上一层所有输入)
前馈神经网络(从前向后单向推进)
循环神经网络(结点自循环)
工作
输入所有特征,用感知机找到描述的线性函数和判断的激活函数,逐层判断,最终选出权重最大的结果
改进
(参考吴恩达)激活函数由 01 改为连续阶跃曲线,从非黑即白改为可能性评估。效果是每次分类不再限于 2 类
组织神经网络过程中,虽然没有给定判断标准,但神经网络会逐渐形成对特征的一种标准描述,用于后续判断数据与标准的偏差。随着训练进程,神经网络的描述能力越发熟练
阶跃曲线在空间也能体现,改变输入特征,每个输出曲面都会变化
总结
-
激活函数赋予了选择过程,使结果不能以一般形式呈现,使得神经网络开始复现人的非线性认知过程
-
目前 AI 的选择有用到统计学,不过未来目标仍然是以人脑为范式
身为 AI 乐观主义者,我认为目前 AI 缺的还是算力,人脑的复杂程度众所周知(我不否认心理上的恐怖谷
仅针对认知过程而言,因为我认为机器结构和细胞生物本身就没有可比性(很长一段时间内
损失函数
损失函数
最小二乘法
- 数据希望得到的标签 $x_i$,神经网络输出的结果 $yi$,直接用 $\sum{i=1}^n(y_i-x_i)^2$ 表示损失
平方是方便后续梯度下降求导,有时前面可以加 $\frac{1}{2}$ 辅助求导
实际使用有限制
极大似然估计法
概率学的内容
当满足条件 $θ$ 时,对于所有可能结果中的一项,概率为 $\prod_{i=1}^kP(C_i|θ)$ ,其中一项发生和其他项不发生是同时出现的,故为概率乘积,对于已知的可能性,选出结果(似然值)最大的一个为最可能的模型
人去判断或估计一件事时,是遵循已存在的认知,神经网络如果能够认知,自然能通过不断尝试,逼近人脑内模型
确定一个模型然后给出似然值,则 $θ$ 与神经网络结点的线性系数 $W,b$ 相关,进而与判断结果 $y_i$ 相关,其中为某个标签 $x_i$ 的概率可以直接用式子表示出来。比如在判断 01 时,判断为 $y_i$ 概率直接变成 $y_i^{x_i}(1-y_i)^{1-x_i}$ 再求 $\prod$
-
然后我们用 log 将 $\prod$ 转为 $\sum$ 就得到了第二种损失函数:$\sum_{i=1}^n(x_i·logy_i+(1-x_i)·log(1-y_i))$
显然要求上式的极大值,但为统一标准,在前面加上负号求极小值
交叉熵
-
信息量
信息量大小可以理解为详细程度,即概率事件变为确定事件需要的“能量”,若在一份确定的基础上再加确定,能得到新的信息量,定义为加法。首先可以确定,信息量越大,概率越小,反相关,概率 < 1,信息量 > 0
设变量 $x$ :发生概率,信息量相加等于概率相乘,$f(x_1·x_2)=f(x_1)+f(x_2)$,相乘变相加是不是似曾相识?所以设 $f(x)$ 为对数使其合理,如果我们以每种 0/1 事件变为确定事件为标准,得到最基本的公式为
$f(x)=-log_2x$,而信息单位恰为 bit
-
熵
熵代表系统不确定度,不确定度又受系统中各个事件影响,将熵定义为系统信息量的期望即可
-
交叉熵
回归主题,要求出两个系统 $p,q$ 的误差,以 $p$ 为基准,关于 $p$ 中的事件概率,根据信息量差值,就可以求两个系统的相对熵 $\sum_{i=1}^mp_i·(f_Q(q_i)-f_P(pi))$,又称 KL 散度 $D{KL}(P||Q)$,去掉 $p$ 的期望熵,剩余的就是交叉熵 $H(P,Q)=\sum_{i=1}^mp_i·(-log_2q_i)$
因为吉布斯不等式(通过放缩证明),上面的相对熵值总是 $\ge0$,因此只考虑单调的交叉熵就可以衡量损失了
在计算时,如果 p 和 q 的事件数量不同,直接以数量更高的为准(分布精细)对相同位置的事件求期望
-
损失函数
我们以图像识别为例,基准 $p$ 可以直接替换为已被确定标签的“可能事件” $x$,即 $p$ 是确定的 0 或 1,总事件数取 $q$ 求期望需要判断的总图像数(更多的 p 和 q 事件数按上面的方法均匀处理就行)
由于考虑信息时 p 和 q 都是确定结果,但实际替换过激活函数的神经网络只会输出一个可信度,需要人为添加一次判断,也就是 $x$ 取标签 0/1 时相应的输出 $y$ 在指定标签上的可信度(比如 0 时就取不可信度)求期望,最终得到
$\sum_{i=1}^mx_i·(-log_2qi)=-\sum{i=1}^m(x_i·log_2y_i+(1-x_i)·log_2(1-y_i))$
这里计算 $1-x_i$ 是因为只有两种情况,非此即彼,遇到更多情况,其实写出来式子也是类似的
可以看出形式和极大似然估计法几乎相同,但这里的信息是有意义的东西,负号也不是后来加上的
梯度下降
反向传播
以感知机为单位,信息传播的基础还是每个线性函数也就是 W b
正向传播由 W b 输出信息,反向传播即将最终的偏差向前逆推从而修正 W b
-
思路 1
比如由第 3 层的某一个输出 $a^{[3]}$ 计算损失函数值 $J$,决定的因素就是接受到的所有第二层的 $W^{[2]}$ $b^{[2]}$ 和第二层输出 $a^{[2]}$
其中 $W$ 和 $b$ 只看上一层,直接发散到上一层各结点的影响权重来修正,前面各层的 $W$ $b$ 类推
而 a 的反向传播会比较深入,上一层 $a^{[i]}$ 每个感知机的修正都由下一层连接的所有 $a^{[i+1]}$ 影响,就反向求权重
最后所有的参数都能获得自己的权重,就可以开始修正工作了
-
思路 2(用梯度)
用向量作衡量,求损失值 $J$ 的梯度 $\nabla J(W,a,b)=(α,β,γ)$,就找到了下降最快的路径,回忆高数计算梯度,设 $(α,β,γ)$ 为 3 变量偏导向量即梯度,$W,a,b$ 各减去 $η$ 倍 $α,β,γ$ 为目标值
可求出 $W$ $b$ 的目标值,再设 $J{前一层}=\beta=a-a{目标}$,就可以由 $a$ 继续向前传播,到达起始层后 $a^{[1]}$ 不再影响损失,最终只剩 $W$ $b$
- 结果很直观,用链式求偏导来求最终 $W$ $b$ 如何被修正
前一层 $a$ 的 $J$ 计算需要当前层 $a$ 的修正值,所以如果有从前向后一传多的情况,求 $J_{前一层}$ 需要求当前层所有偏导 $β$ 的平均值
- 另外,关于 $W^{[i]}$ 和 $b^{[i]}$ 如何得到 $a^{[i+1]}$,设第 $l$ 层第 $i$ 个感知机,先求出每个线性结果 $z^{[l]}_i=W{[l]}_i·a^{[l]_i}+q^{[l]}_i$ 再用激活函数。一组感知机写成矩阵乘法形式就比较简便







